
The exponent of a number indicates the number of times the base number is multiplied by itself. For example,
\[2^4=2\times 2\times 2\times 2 \qquad \text{or} \qquad \left(\frac{1}{2}\right)^2 = \frac{1}{2} \times \frac{1}{2}\]
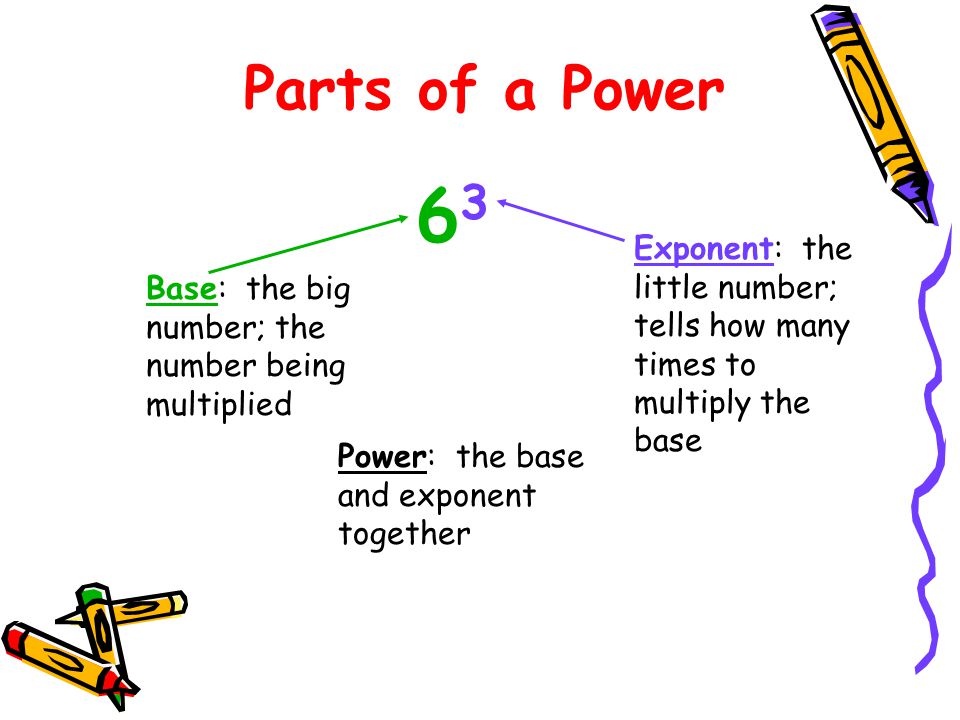
| Name | How it Works | Examples |
|
Product Rule
|
When multiplying two numbers with the same base, you can add their exponents together. \begin{align} a^m \times a^n &= a^{m+n} \end{align} |
\begin{align} 2^2 \times 2^3 &= 2^{2+3} \\ &= 2^5 \\ &= 32 \end{align} \begin{align} 3 \times 3^2 &= 3^{1+2} \\ &= 3^3 \\ &= 27 \end{align} |
|
Quotient Rule
|
When dividing two numbers with the same base, you can subtract their exponents. \begin{align} \dfrac{a^m}{a^n} &= a^m \div a^n \\ &= a^{m-n} \end{align} |
\begin{align} 7^9 \div 7^7 &= 7^{9-7} \\ &= 7^2 \\ &= 49 \end{align} \begin{align} \dfrac{4^{11}}{4^7} &= 4^{11-7} \\ &= 4^4 \\ &= 256 \end{align} |
|
Power of a
Power Rule |
Multiply the exponents together. \begin{align} (a^m)^n = a^{mn} \end{align} |
\begin{align} \left(2^3\right)^4 &= 2^{3\times4} \\ &= 2^{12} \\ &= 4096 \end{align} \begin{align} \left(x^9\right)^2 &= x^{9\times2} \\ &= x^{18} \end{align} |
|
Power of a Product Rule
|
Apply the exponent to each factor in the product. \begin {align} (ab)^m = a^mb^m \end{align} or \begin{align} (abc)^m = a^mb^mc^m \end{align} (no matter how many factors there are, the rule still applies in the exact same way.) |
\begin{align} \left(2^2g^3\right)^3 &= \left(2^2\right)^3\left(g^3\right)^3 \\ &= 2^6g^9 \\ &= 64g^9 \end{align} \begin{align} \left(3x^2y^4\right)^2 &= \left(3^2\right)\left(x^2\right)^2\left(y^4\right)^2 \\ &= 9x^4y^8 \end{align} \begin{align} \left(5xyz^2\right)^3 &= 5^3x^3y^3\left(z^2\right)^3 \\ &= 125x^3y^3z^6 \end{align} |
|
Power of a Quotient Rule
|
Apply the exponent to the numerator and denominator separately. \begin{align} \left(\frac{a}{b}\right)^m &= \dfrac{a^m}{b^m} \end{align} |
\begin{align} \left(\frac{2}{3}\right)^2 &= \dfrac{2^2}{3^2} \\ &= \dfrac{4}{9} \end{align} \begin{align} \left(\frac{4x^2}{3y}\right)^4 &= \dfrac{\left(4x^2\right)^4}{\left(3y\right)^4} \\ |
| Misconception | What Some Students Think | What Actually Happens | Example |
| Adding exponents for different bases | \(2^3\times 3^2=2^{3+2}=2^5\) | Exponents can only be added if bases are the same | \(2^3\times 3^2=2^{3+2}\neq 2^5\); simplify separately |
| Multiplying exponents instead of adding when multiplying bases | \(2^3\times 2^4=2^{3\times 3}=2^12\) | Multiplying same bases implies adding exponents, not multiplying | \(2^3\times 2^4=2^{3+4}=2^7\) |
| Negative exponents make the base negative | \(2^{-3}=-2^3\) | Negative exponent means reciprocal, not negative base | \(2^{-3}=\frac{1}{2^3}=\frac{1}{8}\) |
| Zero exponent makes base zero | \(0^0=0\) | \(a^0=1\) for \(a\neq 0\); \(0^0\) is undefined | Avoid \(0^0\) confusion |
| Distributing exponent over addition incorrectly | \((a+b)^n=a^n+b^n\) | Powers do NOT distribute over addition | \((2+3)^2\neq 2^2+3^2\) since \(5^2=25 \neq 4+9\) |
A negative exponent signals a reciprocal of the base and exponents. Once the reciprocal is performed, the negative exponent becomes positive.
\[2^{-3}=\frac{1}{2^3}=\frac{1}{8}\]
This can also be interpreted as moving a value from the top of the fraction to the bottom and vice versa.
\[\frac{1}{4^{-3}}=\frac{4^3}{1}=64\qquad \frac{3^{-5}}{2^{-2}} = \frac{2^{2}}{3^{5}} = \frac{4}{243} \]
Any base to the exponent of 1 equals itself.
\[13^1=13 \qquad \pi^1=\pi \qquad (2.2)^1=2.2\]
Any non-zero number with the exponent 0 equals to 1.
\[5^0=1 \qquad x^0=1 \qquad \left(\frac{17}{19}\right)^0=1 \qquad \left(-4\right)^0 = 1\]
Simplify without a calculator:
\[\left(2^3\right)^4\times2^{-5}\]
Prompts:
Simplify and write with positive exponents:
\[\frac{\left( 3^2\times 3^{-5}\right) ^3}{3^{-4}}\]
Prompts:
True or Fale - Explain your reasoning:
\[\left( 5^2+5^3\right) ^2=5^{(2+3)\times 2}\]
Simplify the expression:
\[\frac{\left(x^4y^{-2}\right) ^3}{x^{-5}y^3}\]
Prompts:
Simplify if possible (or explain why not):
\[\frac{\left( (3x+2)^4\times(3x+2)^{-2}\right)}{(3x+2)^3}\]
Prompts:
Simplify or explain why the operation is invalid:
\[(2x^2+1)^3\times(2x^2+1)^{-\frac{5}{2}}\times (2x^2+1)^{\frac{1}{2}}\]

Designed by Matthew Cheung. This work is licensed under a Creative Commons Attribution 4.0 International License.