
Question: Would you rather receive $10,000 a day for a month or one penny ($0.01) that doubles every day for a month?
You might choose the $10,000 at first, but you'll see that with the magic of compounding, the doubling penny option would earn you a whopping $10,737,418 while the $10,000 every day would only make you $310,000 richer. This means that the penny would earn almost 35X the amount that the $10,000 did!
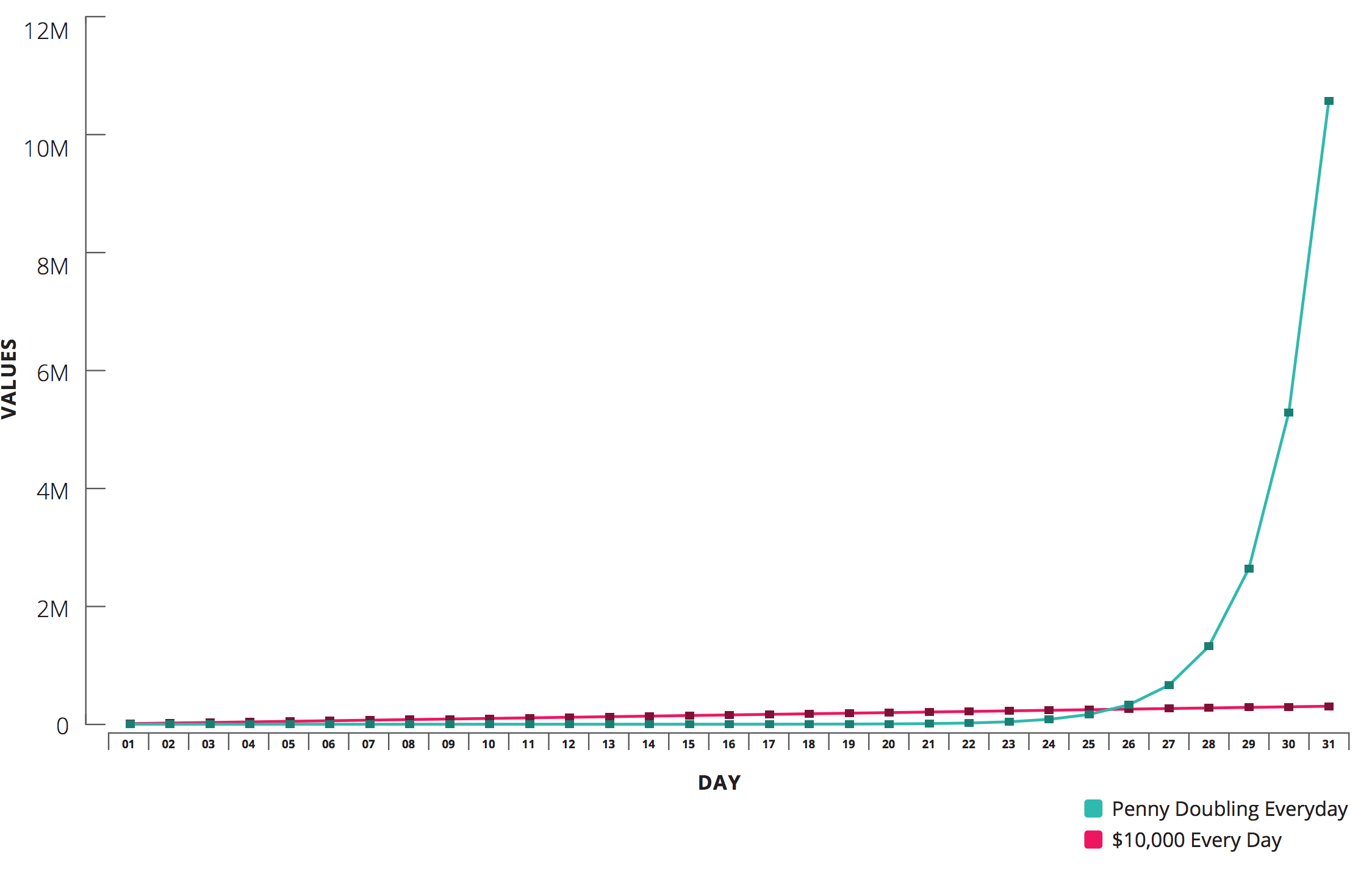
Reference: https://napkinfinance.com/napkin/compound-interest-definition/
Interest that is earned on both the initial principal amount and the interest accrued in previous periods during the investment/loan term is called compound interest. In other words, it can be seen as "interest on interest" - hence the name compound interest. Unlike simple interest, compound interest grows exponentially (while simple interest grows linearly), making it a common method of earning interest when investing or borrowing money.
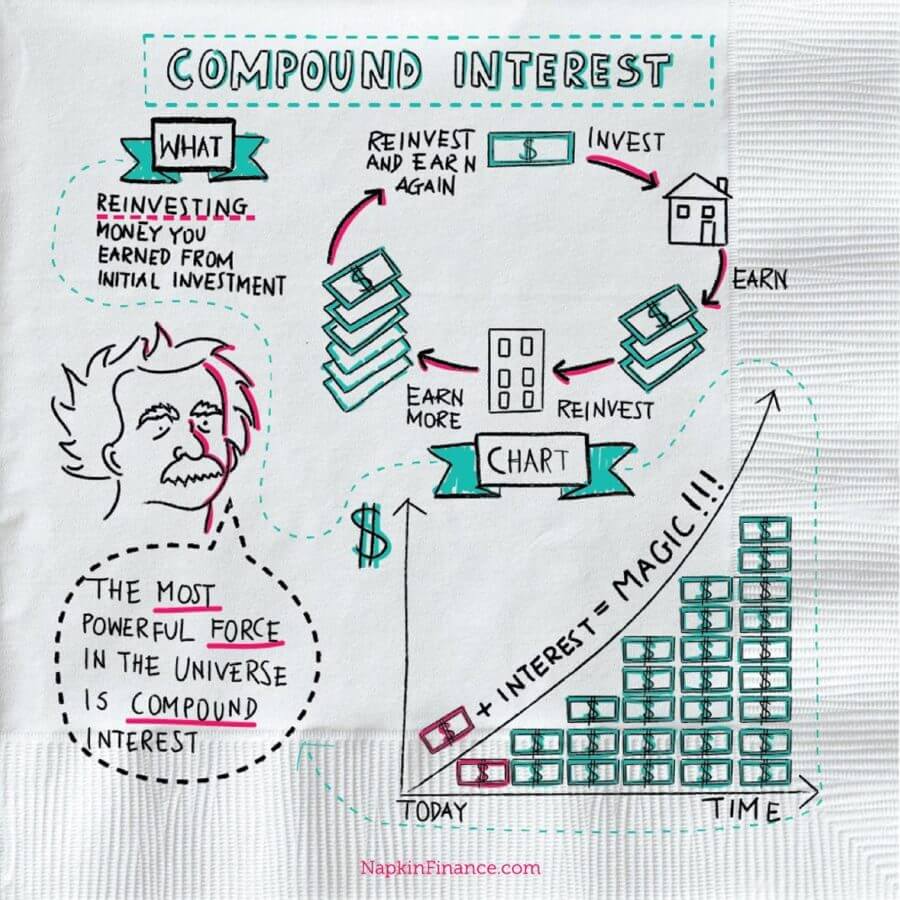
(Image from https://napkinfinance.com/napkin/compound-interest-definition/)
To calculate compound interest, we have to consider the original amount of money, called principal (present value), the time (period over which the money is being used), the length and number of compounding periods (details below), and the (compound) interest rate. Taking these factors into account, we can use the following formula to calculate the maturity/future value of an amount earning compound interest:
\(S=P(1+i)^n\),
where:
Tip: We can also rearrange the above formula to solve for \(P\), the principal (present value):
\(P=S(1+i)^{-n}\)
Compounding Periods
The following table shows common compounding frequencies/periods, their durations, how many times each period occurs per year, and how to calculate the interest rates per compounding period given the annual interest rate:

The following examples will demonstrate how we can use the formulas introduced in the previous section.
Example 1
Solution
First, we can identify the information that is given in the problem. For both options, we have:
\(P=25,000, t=6\) years
| Investment A | Investment B |
|
Given information: \(i=\frac{0.084}{26}, n=26 \times 6 = 156\) Calculation: \(S=25000(1+\frac{0.084}{26})^{156}=41349.63\) Maturity Value: \($41,349.63\) Interest Earned: \($41,349.63-$25,000=\) \($16,349.63\) |
Given information: \(i=\frac{0.075}{12}=0.00625,n=12 \times 6=72\) Calculation: \(S=25000(1+0.00625)^{72}=39152.94\) Maturity Value: \($39,152.94\) Interest Earned: \($39,152.94-$25,000=\) \($14,152.94\) |
Comparing the two maturity values we get for both options, we find that Marina should choose Investment A, and she will earn \($16,349.63-$14,152.94=\) \($2196.69\) more in interest with this option.
Example 2
Solution
Since we're looking for the amount invested, we are determining the principal amount or \(P\).
First, we can identify the information that is given in the problem:
\(S=15,000, i=\frac{0.0475}{4}=0.011875, n=6\times 4=24\)
Substituting these values into the compound interest formula gives:
\(15000=P(1+0.011875)^{24}\)
Then, we can isolate for \(P\):
\(P=\frac{15000}{(1+0.011875)^{24}}\)
\(=11299.17\)
So, \($11, 299.17\) must be invested to reach the required maturity value.
Example 3
Solution
See the video below for the solution!
Tip: This solution will use the ideas of equivalent values and setting focal dates (To review these concepts, see Equivalent Values).