Exponential and Logarithmic Functions

There are various real-life applications that can be modelled using exponential/logarithmic functions.

For exponential functions, these include: population growth compound interest isotope halflife.

For logarithmic functions, these include: hydrogen ion concentration (pH scale) earthquake intensity (Richter scale) sound intensity (decibel scale).

We will describe a few of these applications and work through some related word-problem examples in the following sections.

                                                                

Data such as population can be modeled using exponential growth/decay. The general formula used in modeling and calculations involving exponential growth/decay is:

\(A=A_0b^t\),

where:

• \(A\) is the total value/amount,
• \(A_0\) is the initial value/amount,
• \(b\) is the factor of growth/decay (calculated as \(b=1+r\) for growth rate \(r\) or \(b=1-r\) for decay rate \(r\)),
• \(t\) is the number of time periods

We will use this formula in the following example:

Solution:

a) Since the rate of growth is \(r=2.5\%=0.025\), the growth factor is \(b=1+r=1+0.025=\)\(1.025\).

b) From the information given in the question, we have that \(A_0=45000\), and that the growth factor is \(b=1.025\) (from part a)). Substituting these values into the general formula gives:

\(A=45000(1.025)^t\), where \(t\) is the number of years after 2015

c) Since 2025 is 10 years after 2015, \(t=10\). Substituting this value into the equation we found in part b) gives the estimate for the population of Apple County in 2025:

\(A=45000(1.025)^{10}= \ \)\(57604\)

Many radioactive isotopic substances' masses decrease over time, and a useful piece of information when working with such substances in chemistry is their half-life - the amount of time required for an amount to decrease to half its initial quantity. A general formula used when doing calculations involving half-life is:

\(M=A(\frac{1}{2})^{\frac{t}{h}}\), 

where:

• \(M\) is the remaining or current mass/amount,
• \(A\) is the initial amount/mass,
• \(t\) is the time elapsed,
• \(h\) is the half-life.

We will use this formula in the following example:

Solution:

From the information given in the question, we have that \(A=350, M=23.5, t=14 (days)\). So substituting these values into the general formula and solving for the half-life \(h\) gives:

\(23.5=350(\frac{1}{2})^{\frac{14}{h}}\)

\(\frac{23.5}{350}=(\frac{1}{2})^{\frac{14}{h}}\)

\(\frac{47}{700}=(\frac{1}{2})^{\frac{14}{h}}\)

\(\frac{14}{h}=log_{\frac{1}{2}}(\frac{47}{700})=\frac{log(\frac{47}{700})}{log(\frac{1}{2})} \approx 3.90\)

\(h=\frac{14}{3.90}=\)\(\ 3.59\)

So, the half-life of radium is 3.59 days (this means that after 3.59 days, there will only remain half of the original amount of radium).

The pH scale, often used in chemistry, measures a substance's acidity or alkalinity by giving it a pH value of 0 to 14. The concentration of hydrogen ions (compared to a substance with pH of 7) in a substance is directly related to its pH value, specifically, it follows the below relationship/equation:

\(pH=-log[H^+]\),

where:

• \(pH\) is the pH value (number between 0-14),
• \([H^+]\) is the concentration of hydrogen ions (measured in mol/L).

Note: Every difference of one between pH values corresponds to a tenfold (or 10 times) change in the concentration of hydrogen ions in a substance, hence the use of a logarithmic scale (of base 10). 

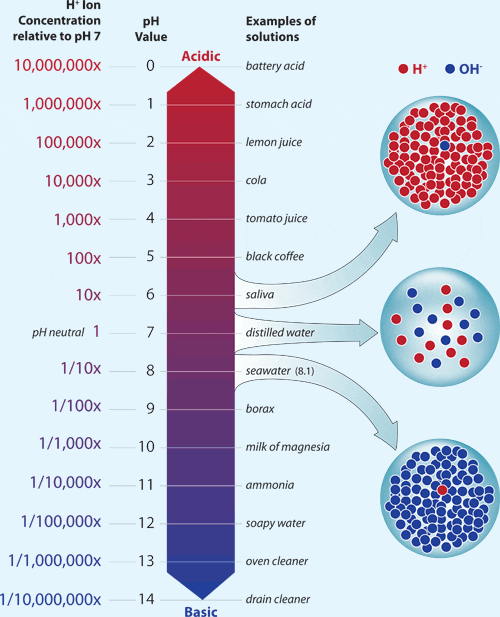
(Image: https://www.whoi.edu/know-your-ocean/ocean-topics/ocean-chemistry/ocean-acidification/the-ph-scale/)

We will use this formula in the following examples:

Solution: We're given that \([H^+]=0.00002\), so substituting this value into the \(pH\)-\([H^+]\) equation gives the pH value of:

\(pH=-log(0.00002) \approx\)\(4.7\)

 

Solution: We're given that pH = 4, so substituting this value into the \(pH\)-\([H^+]\) equation and solving for \([H^+]\) gives:

\(4=-log[H^+]\)

\(-4=log[H^+]\)

\([H^+]=10^{-4}=\)\(0.0001 mol/L\)

 

Solution: We first find the hydrogen ion concentrations of both acids by using the \(pH\)-\([H^+]\) equation, then use their pH values to compare their acidity strength.

Acid with pH 1.4	Acid with pH 2.6
\(1.4=-log[H^+]\) \(-1.4=log[H^+]\) \([H^+]=10^{-1.4} \approx 0.03981\)	\(2.6=-log[H^+]\) \(-2.6=log[H^+]\) \([H^+]=10^{-2.6} \approx 0.00251\)

To compare the strength of the first acid with the second, we divide the hydrogen ion concentration of the first acid by the concentration of the second:

\(\frac{0.03981}{0.00251} \approx 15.86\)

So, an acid with a pH of 1.4 is approximately \(15.86\) times stronger than one with pH of 2.6.

Designed by Matthew Cheung. This work is licensed under a Creative Commons Attribution 4.0 International License.