
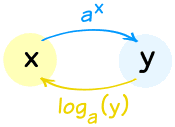
Recall that we can write logarithmic functions in two different, but equivalent, forms: exponential form and logarithmic form (recall the detailed definitions here). So, it is important to know how to switch between these two forms as it will be helpful when solving equations or when graphing logarithmic functions.
(image from https://www.mathsisfun.com/algebra/exponents-logarithms.html)
By definition, we have:
\(y=b^x \iff log_b(y)=x\)
and we will use this fact in the below examples relating to converting between exponential and logarithmic form.
Solution:
To convert from logarithmic to exponential form, we recall the general formula:
\(log_b(y)=x \Rightarrow y=b^x\)
In this case, we have the following values from the logarithmic equation:
\(b=7, y=\sqrt{343}, x=\frac{3}{2}\)
So we can substitute these values into the exponential form \(b^x=y\) (which is the same as \(y=b^x\)) to get the exponential form of \(log_7(\sqrt{343})=\frac{3}{2}\):
\(7^{\frac{3}{2}}=\sqrt{343}\)
Solution:
Since we want to find the value of \(log_3(81)\), in other words, we want to find the \(?\) in \(log_3(81)= \\ ?\).
Rewriting this in exponential form gives us:
\(3^?=81\)
So, we're trying to find the exponent we have to raise 3 to, in order to get 81. We can either find this exponent by trial and error (e.g. multiply 3 by itself multiple times until we reach 81, testing different exponent values) or by noticing that \(3^2=9\) and \(9^2=81\), so \((3^2)^2=3^4=81\).
This gives us that the \(?\) in \(3^?=81\) is \(4\), and so the value of \(log_3(81)=4\).
Solution:
To convert from exponential to logarithmic form, we recall the general formula:
\(y=b^x \Rightarrow log_b(y)=x\)
In this case, we have the following values from the exponential equation:
\(y=\frac{1}{4}, b=2, x=-2\)
So we can substitute these values into the logarithmic form \(log_b(y)=x\) to find the logarithmic form of \(2^{-2}=\frac{1}{4}\):
\(log_2(\frac{1}{4})=-2\)
