Library Guides: Trigonometry: Angles in Standard Positions

The section Unit Circle showed the placement of degrees and radians in the coordinate plane. Angles in the unit circle start on the x-axis and are measured counterclockwise about the origin. While these unit circle concepts are still in play, we will now not be "drawing" the unit circle in each diagram. Our diagrams will now allow us to work with radii exceeding the unit one (as seen in the unit circle).

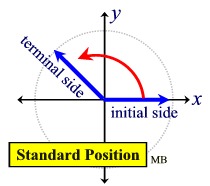
Standard Position: An angle is in standard position if its vertex is located at the origin and one ray is on the positive x-axis. The ray on the x-axis is called the initial side and the other ray is called the terminal side. If the terminal side of an angle lies "on" the axes (such as 0º, 90º, 180º, 270º, 360º ), it is called a quadrantal angle. The angle shown at the right is referred to as a Quadrant II angle since its terminal side lies in Quadrant II.

The angle is measured by the amount of rotation from the initial side to the terminal side. If measured in a counterclockwise direction the measurement is positive. If measured in a clockwise direction the measurement is negative. (A negative associated with an angle's measure refers to its "direction" of measurement, clockwise.)

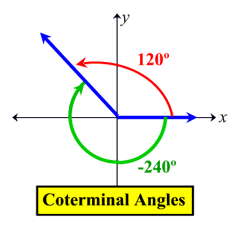
If two angles in standard position have the same terminal side, they are called coterminal angles. In the diagram at the left, +120º and -240º are coterminal angles.

Draw the following angles. Include the terminal arms and direction of angle.

210º

-72º

510º

You can verify angle locations using this website.

Key questions to consider:

Where is the Initial Side always located?

How does the direction of the graph relate to +/- sign of the angle?

What happens when you exceed a full rotation (360º)?

How many times can you go around?

Reference: https://mathbitsnotebook.com/Algebra2/TrigConcepts/TCStandardPosition.html

Designed by Matthew Cheung. This work is licensed under a Creative Commons Attribution 4.0 International License.